DUT人工智能与专家系统_HW1

1 采用广度优先搜索(BFS)、深度优先搜索(DFS)编程求解八数码问题（初始状态允许任意），找出一种从初始状态到目标状态移动步数最少的步骤。

八数码难题是一种经典的拼图游戏，也称为九宫格问题。它的目标是将一个 3x3 的方格拼图按照指定的顺序排列。每个方格上都有一个数字，其中一个方格为空，可以与相邻的方格交换位置。例如，以下是一个八数码难题的初始状态和目标状态：

1
2
3
4
初始状态：   目标状态：
2 8 3        1 2 3
1 0 4   ->   8 0 4
7 6 5        7 6 5

八数码难题最早出现在19世纪末期，当时它被称为“九宫格问题”，是由美国的一位数学家Sam Loyd发明的。他将数字1到8排列在一个3x3的方格中，留下一个空格，要求将数字重新排列，使得数字从左到右、从上到下依次排列。这个问题在当时引起了很大的轰动，成为了一种流行的智力游戏。

八数码难题在计算机科学中也有着广泛的应用。它是人工智能领域中的一个经典问题，可以用来测试搜索算法的性能和效率。八数码难题也被用来研究人类的思维过程和决策行为。此外，八数码难题还被应用于密码学和安全领域，例如用于生成随机数列和加密算法。

八数码难题的解法可以通过搜索算法来实现。搜索算法是一种通过遍历状态空间来寻找解决问题的方法。在八数码难题中，状态空间是所有可能的状态的集合，每个状态表示为一个3x3的矩阵。搜索算法可以通过遍历状态空间来找到从初始状态到目标状态的路径，即解决方案。

常用的搜索算法包括深度优先算法、广度优先算法、A*算法等。这些算法在八数码难题中的表现不同，具有不同的优缺点。例如，深度优先算法可以实现内存占用小，但可能会陷入局部最优解；广度优先算法可以保证找到最优解，但需要更多的内存空间。

除了搜索算法，还有一些其他的解法可以用来解决八数码难题，例如启发式搜索、模拟退火等。这些方法可以通过引入启发式函数、随机化等技术来提高搜索效率和解决复杂问题。

总之，八数码难题是一个经典的拼图游戏，具有广泛的应用价值。通过搜索算法和其他解法，我们可以找到从初始状态到目标状态的路径，解决这个问题。在计算机科学和人工智能领域，八数码难题是一个重要的研究对象，可以帮助我们更好地理解和应用搜索算法、人工智能和机器学习等技术。

1.1 BSF求解八数码问题

广度优先搜索 （BFS） 算法，从它的名字“广度”开始，通过节点的外边缘发现节点的所有邻居，然后通过它们的外边缘发现前面提到的邻居的未访问邻居，依此类推，直到访问从原始源访问的所有节点（如果还有剩余的未访问节点，我们可以继续并采用另一个原始源，依此类推）。这就是为什么如果边的权重是均匀的，它可以用来找到从一个节点（原始源）到另一个节点的最短路径（如果有的话）。

在八数码难题中，广度优先算法会从初始状态开始，先将所有与初始状态相邻的状态加入队列，然后遍历这些状态相邻的状态，以此类推，直到找到目标状态或者遍历完整个状态空间。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# BSF
from collections import deque
# 定义目标状态
goal_state = [1, 2, 3, 4, 5, 6, 7, 8, 0]  # 0代表空格
# 计算当前状态的可行动作
def get_actions(state):
    actions = []
    empty_index = state.index(0)
    if empty_index % 3 > 0:
        actions.append('left')
    if empty_index % 3 < 2:
        actions.append('right')
    if empty_index >= 3:
        actions.append('up')
    if empty_index < 6:
        actions.append('down')
    return actions
# 执行动作，生成新状态
def move(state, action):
    new_state = state[:]
    empty_index = new_state.index(0)
    if action == 'left':
        new_state[empty_index], new_state[empty_index - 1] = new_state[empty_index - 1], new_state[empty_index]
    elif action == 'right':
        new_state[empty_index], new_state[empty_index + 1] = new_state[empty_index + 1], new_state[empty_index]
    elif action == 'up':
        new_state[empty_index], new_state[empty_index - 3] = new_state[empty_index - 3], new_state[empty_index]
    elif action == 'down':
        new_state[empty_index], new_state[empty_index + 3] = new_state[empty_index + 3], new_state[empty_index]
    return new_state
# 广度优先搜索
def bfs(initial_state):
    queue = deque([(initial_state, [])])
    visited = set()
    while queue:
        state, path = queue.popleft()
        visited.add(tuple(state))
        if state == goal_state:
            return path
        for action in get_actions(state):
            new_state = move(state, action)
            if tuple(new_state) not in visited:
                queue.append((new_state, path + [action]))
    return None
# 测试
if __name__ == "__main__":
    initial_state = [7, 2, 4, 5, 0, 6, 8, 3, 1]  # 初始状态
    solution = bfs(initial_state)
    if solution:
        print("Solution found in", len(solution), "steps:", solution)
    else:
        print("No solution found.")

输出如下：

1.2 DSF求解八数码问题

深度优先搜索 （DFS） 算法，从其名称“深度”开始，通过其外边缘发现最近发现的节点 x 的未访问邻居。如果节点 x 没有未访问的邻居，则算法回溯以发现节点 x 的节点的未访问邻居（通过其外部边缘），依此类推，直到访问从原始源访问的所有节点（如果还有剩余的未访问节点，我们可以继续并采用另一个原始源，依此类推）。

在八数码难题中，深度优先算法会从初始状态开始，选择一个数字，将其与空格交换位置，然后继续向下搜索，直到找到目标状态或者无法继续为止。如果无法继续，算法会回溯到上一个节点，继续搜索其他方向。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# DSF
# 定义目标状态
goal_state = [1, 2, 3, 4, 5, 6, 7, 8, 0]  # 0代表空格
# 计算当前状态的可行动作
def get_actions(state):
    actions = []
    empty_index = state.index(0)
    if empty_index % 3 > 0:
        actions.append('left')
    if empty_index % 3 < 2:
        actions.append('right')
    if empty_index >= 3:
        actions.append('up')
    if empty_index < 6:
        actions.append('down')
    return actions
# 执行动作，生成新状态
def move(state, action):
    new_state = state[:]
    empty_index = new_state.index(0)
    if action == 'left':
        new_state[empty_index], new_state[empty_index - 1] = new_state[empty_index - 1], new_state[empty_index]
    elif action == 'right':
        new_state[empty_index], new_state[empty_index + 1] = new_state[empty_index + 1], new_state[empty_index]
    elif action == 'up':
        new_state[empty_index], new_state[empty_index - 3] = new_state[empty_index - 3], new_state[empty_index]
    elif action == 'down':
        new_state[empty_index], new_state[empty_index + 3] = new_state[empty_index + 3], new_state[empty_index]
    return new_state
# 深度优先搜索
def dfs(state, path, visited, depth_limit):
    if state == goal_state:
        return path
    if len(path) >= depth_limit:
        return None
    visited.add(tuple(state))
    for action in get_actions(state):
        new_state = move(state, action)
        if tuple(new_state) not in visited:
            result = dfs(new_state, path + [action], visited, depth_limit)
            if result:
                return result
    return None
# 测试
if __name__ == "__main__":
    initial_state = [7, 2, 4, 5, 0, 6, 8, 3, 1]  # 初始状态
    max_depth = 30  # 深度限制
    solution = None
    for depth in range(1, max_depth + 1):
        visited = set()
        solution = dfs(initial_state, [], visited, depth)
        if solution:
            break
    if solution:
        print("Solution found in", len(solution), "steps:", solution)
    else:
        print("No solution found within depth limit.")

输出如下：

2 分啤酒问题(状态空间搜索问题) 现有8升、5升、3升的容器各一个，均无任何度量标记，其中8升的容器装满啤酒，其他两个为空。要求用上述容器倒来倒去，分成两份4升的啤酒。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
# 定义目标状态
goal_state = (4, 4, 0)
# 获取当前状态可行的倒酒操作
def get_actions(state):
    actions = []
    x, y, z = state
    # 倒酒操作：
    # 1. 从x到y
    if x > 0 and y < 5:
        actions.append(('x', 'y'))
    # 2. 从x到z
    if x > 0 and z < 3:
        actions.append(('x', 'z'))
    # 3. 从y到x
    if y > 0 and x < 8:
        actions.append(('y', 'x'))
    # 4. 从y到z
    if y > 0 and z < 3:
        actions.append(('y', 'z'))
    # 5. 从z到x
    if z > 0 and x < 8:
        actions.append(('z', 'x'))
    # 6. 从z到y
    if z > 0 and y < 5:
        actions.append(('z', 'y'))
    return actions
# 执行倒酒操作，生成新状态
def pour(state, action):
    x, y, z = state
    from_vessel, to_vessel = action
    if from_vessel == 'x' and to_vessel == 'y':
        amount = min(x, 5 - y)
        return (x - amount, y + amount, z)
    elif from_vessel == 'x' and to_vessel == 'z':
        amount = min(x, 3 - z)
        return (x - amount, y, z + amount)
    elif from_vessel == 'y' and to_vessel == 'x':
        amount = min(y, 8 - x)
        return (x + amount, y - amount, z)
    elif from_vessel == 'y' and to_vessel == 'z':
        amount = min(y, 3 - z)
        return (x, y - amount, z + amount)
    elif from_vessel == 'z' and to_vessel == 'x':
        amount = min(z, 8 - x)
        return (x + amount, y, z - amount)
    elif from_vessel == 'z' and to_vessel == 'y':
        amount = min(z, 5 - y)
        return (x, y + amount, z - amount)
# 深度优先搜索
def dfs(state, path, visited):
    if state == goal_state:
        return path
    visited.add(state)
    for action in get_actions(state):
        new_state = pour(state, action)
        if new_state not in visited:
            result = dfs(new_state, path + [action], visited)
            if result:
                return result
    return None
# 测试
if __name__ == "__main__":
    initial_state = (8, 0, 0)  # 初始状态（8升容器中装满）
    visited = set()
    solution = dfs(initial_state, [], visited)
    if solution:
        print("Solution found in", len(solution), "steps:", solution)
    else:
        print("No solution found.")

输出如下：

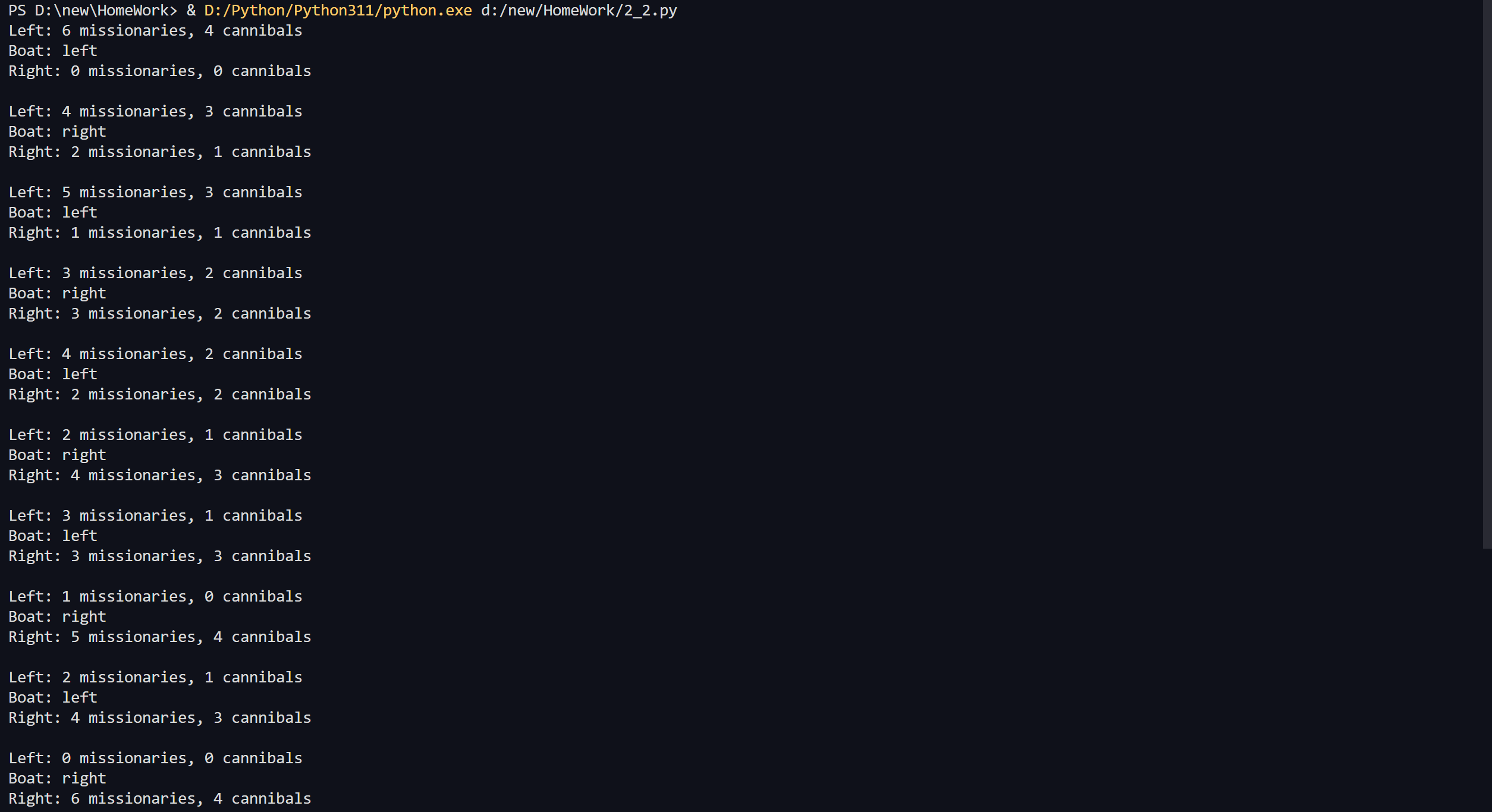
3 传教士和野人过河问题(启发式搜索算法)： 有N个传教士和N个野人来到河边渡河，河岸有一条船，每次至多可供k人乘渡。问传教士为了安全起见，应规划摆渡方案，使得任何时刻，传教士和野人在一起时河两岸及船上的野人数目总是不超过传教士的数目(否则传教士有可能被野人吃掉)。求解传教士和野人从左岸全部摆渡到右岸的过程中，任何时刻传教士和野人在一起时，满足传教士数大于或等于野人数，并且两者人数之和小于k的摆渡方案。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
import heapq
class State:
    def __init__(self, left_missionaries, left_cannibals, boat, right_missionaries, right_cannibals, parent=None):
        self.left_missionaries = left_missionaries  # 左岸传教士数量
        self.left_cannibals = left_cannibals  # 左岸野人数量
        self.boat = boat  # 船的位置，'left'表示在左岸，'right'表示在右岸
        self.right_missionaries = right_missionaries  # 右岸传教士数量
        self.right_cannibals = right_cannibals  # 右岸野人数量
        self.parent = parent  # 父状态
    def is_valid(self):
        # 判断状态是否合法，即各个岸上的传教士和野人数目是否符合规则
        if self.left_missionaries < 0 or self.left_cannibals < 0 or self.right_missionaries < 0 or self.right_cannibals < 0:
            return False
        if self.left_missionaries > 0 and self.left_cannibals > self.left_missionaries:
            return False
        if self.right_missionaries > 0 and self.right_cannibals > self.right_missionaries:
            return False
        return True
    def is_goal(self):
        # 判断是否达到目标状态，即左岸没有传教士和野人
        return self.left_missionaries == 0 and self.left_cannibals == 0
    def __eq__(self, other):
        # 判断两个状态是否相等，用于集合去重
        return self.left_missionaries == other.left_missionaries and \
               self.left_cannibals == other.left_cannibals and \
               self.boat == other.boat and \
               self.right_missionaries == other.right_missionaries and \
               self.right_cannibals == other.right_cannibals
    def __hash__(self):
        # 哈希函数，用于集合去重
        return hash((self.left_missionaries, self.left_cannibals, self.boat, self.right_missionaries, self.right_cannibals))
    def __lt__(self, other):
        return False  # dummy implementation for A* algorithm
def get_actions(state, k):
    # 获取当前状态可行的动作列表
    actions = []
    if state.boat == 'left':
        for i in range(1, k + 1):
            for j in range(i + 1):
                if 0 < j <= i:
                    actions.append((i - j, j, 'right'))  # 从左岸到右岸，带走i-j个传教士和j个野人
    else:
        for i in range(1, k + 1):
            for j in range(i + 1):
                if 0 < j <= i:
                    actions.append((j, i - j, 'left'))  # 从右岸到左岸，带走j个传教士和i-j个野人
    return actions
def transition(state, action):
    # 根据动作执行状态转移
    if state.boat == 'left':
        return State(state.left_missionaries - action[0], state.left_cannibals - action[1], action[2],
                     state.right_missionaries + action[0], state.right_cannibals + action[1], state)
    else:
        return State(state.left_missionaries + action[0], state.left_cannibals + action[1], action[2],
                     state.right_missionaries - action[0], state.right_cannibals - action[1], state)
def heuristic(state):
    # 启发式函数，用于估计当前状态到目标状态的距离
    return state.left_missionaries + state.left_cannibals
def astar(start_state, k):
    open_list = []  # 开放列表
    closed_set = set()  # 关闭列表，用于记录已经访问过的状态
    heapq.heappush(open_list, (heuristic(start_state), start_state))  # 将初始状态加入开放列表
    while open_list:
        _, current_state = heapq.heappop(open_list)  # 从开放列表中取出启发式评估值最小的状态
        if current_state.is_goal():  # 如果当前状态是目标状态，返回当前状态
            return current_state
        closed_set.add(current_state)  # 将当前状态加入关闭列表
        for action in get_actions(current_state, k):  # 获取当前状态可行的动作列表
            new_state = transition(current_state, action)  # 根据动作执行状态转移
            if new_state.is_valid() and new_state not in closed_set:  # 如果新状态合法且未被访问过
                heapq.heappush(open_list, (heuristic(new_state), new_state))  # 将新状态加入开放列表
    return None  # 如果找不到解，则返回None
def print_solution(solution):
    if not solution:
        print("No solution found.")  # 如果找不到解，输出提示信息
        return
    path = []
    while solution:
        path.append(solution)
        solution = solution.parent
    for i in range(len(path) - 1, -1, -1):  # 从后向前遍历路径，打印每个状态
        state = path[i]
        print(f'Left: {state.left_missionaries} missionaries, {state.left_cannibals} cannibals')
        print(f'Boat: {"left" if state.boat == "left" else "right"}')
        print(f'Right: {state.right_missionaries} missionaries, {state.right_cannibals} cannibals')
        print()
if __name__ == "__main__":
    # 设置初始状态和船的容量
    start_state = State(6, 4, 'left', 0, 0)
    k = 3
    # 使用A*算法求解
    solution = astar(start_state, k)
    # 打印解决方案
    print_solution(solution)

输出如下：

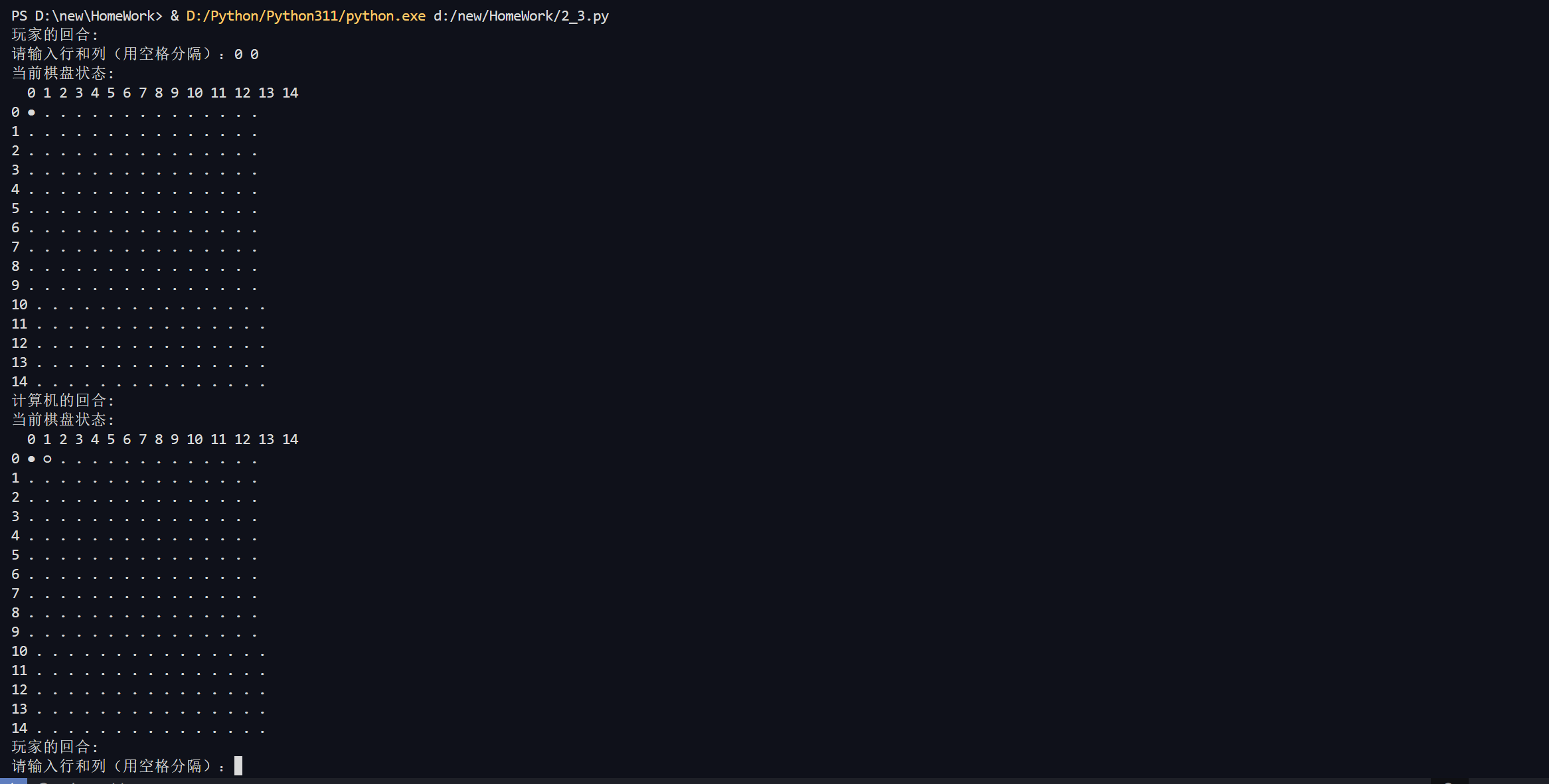
4 人机对战五子棋游戏(博弈搜索α-β剪枝策略) :五子棋的专用棋盘为15路(15╳15)，盘面上横竖各15条、平行线、纵横、线路为黑色，构成225个交叉点。游戏规则：先手无限制，在对局开始时，先由执黑棋的一方将一枚棋子落在天元点上，然后由执白棋的一方在黑棋周围的交叉点上落子。此后，由执黑棋的一方在以天元为中心的25个交叉点的范围内，下盘面的第三手棋。然后由执白棋的一方应手，即下盘面的第四手棋。以后如此轮流落子，直到某一方首先在棋盘的直线、横线或斜线上形成连续5子或5子以上，则该方就算获胜。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
import numpy as np

# 定义棋盘大小
BOARD_SIZE = 15

# 初始化棋盘
def init_board():
    return np.zeros((BOARD_SIZE, BOARD_SIZE), dtype=int)

# 打印棋盘
def print_board(board):
    print("  ", end="")
    for i in range(BOARD_SIZE):
        print(i, end=" ")
    print()
    for i, row in enumerate(board):
        print(i, end=" ")
        for j in range(BOARD_SIZE):
            print("●" if row[j] == 1 else "○" if row[j] == -1 else ".", end=" ")
        print()

# 检查是否有胜者
def check_win(board, player):
    for x in range(BOARD_SIZE):
        for y in range(BOARD_SIZE):
            # 检查横向
            if x + 4 < BOARD_SIZE and all(board[x+i][y] == player for i in range(5)):
                return True
            # 检查纵向
            if y + 4 < BOARD_SIZE and all(board[x][y+i] == player for i in range(5)):
                return True
            # 检查主对角线
            if x + 4 < BOARD_SIZE and y + 4 < BOARD_SIZE and all(board[x+i][y+i] == player for i in range(5)):
                return True
            # 检查副对角线
            if x + 4 < BOARD_SIZE and y - 4 >= 0 and all(board[x+i][y-i] == player for i in range(5)):
                return True
    return False

# 检查是否可以在指定位置落子
def is_valid_move(board, x, y):
    return 0 <= x < BOARD_SIZE and 0 <= y < BOARD_SIZE and board[x][y] == 0

# α-β剪枝
def alpha_beta_search(board, depth, player, alpha, beta, max_player):
    if depth == 0 or check_win(board, player):
        return evaluate(board, player), None

    best_score = None
    best_move = None
    for x in range(BOARD_SIZE):
        for y in range(BOARD_SIZE):
            if is_valid_move(board, x, y):
                new_board = np.copy(board)
                new_board[x][y] = player
                score, _ = alpha_beta_search(new_board, depth - 1, -player, alpha, beta, max_player)
                if player == max_player:
                    if best_score is None or score > best_score:
                        best_score = score
                        best_move = (x, y)
                    alpha = max(alpha, score)
                    if beta <= alpha:
                        break
                else:
                    if best_score is None or score < best_score:
                        best_score = score
                        best_move = (x, y)
                    beta = min(beta, score)
                    if alpha >= beta:
                        break
    return (best_score, best_move)

# 评估当前棋盘状态
def evaluate(board, player):
    # 评分规则可以根据实际情况进行调整
    # 这里简单地给黑方和白方分别赋值为1和-1
    return 1 if player == 1 else -1

# 人机对战
def play_game():
    board = init_board()
    current_player = 1  # 黑方先手
    while not check_win(board, 1) and not check_win(board, -1):
        if current_player == 1:
            print("玩家的回合:")
            x, y = map(int, input("请输入行和列（用空格分隔）：").split())
            while not is_valid_move(board, x, y):
                print("无效的落子位置，请重新输入.")
                x, y = map(int, input("请输入行和列（用空格分隔）：").split())
            board[x][y] = current_player
            print("当前棋盘状态:")
            print_board(board)
            if check_win(board, current_player):
                print(f"恭喜，玩家获胜!")
                break
        else:
            print("计算机的回合:")
            _, best_move = alpha_beta_search(board, 1, -current_player, -float("inf"), float("inf"), current_player)
            x, y = best_move
            board[x][y] = current_player
            print("当前棋盘状态:")
            print_board(board)
            if check_win(board, current_player):
                print(f"遗憾，计算机获胜!")
                break
        current_player = -current_player

# 开始游戏
play_game()

输出如下：

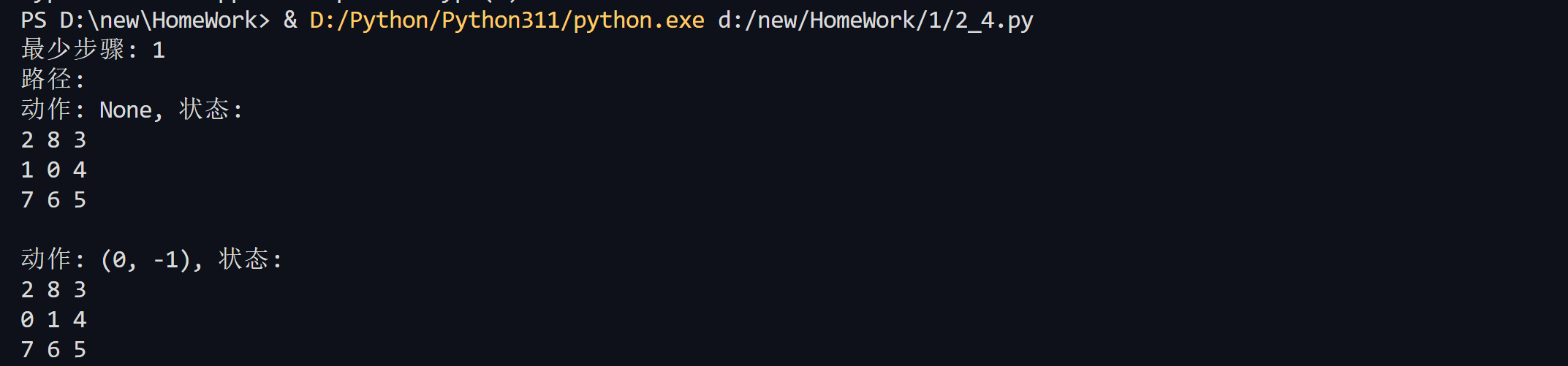
5 求解八数码问题(启发式搜索）在3×3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空的，其初始状态如图所示，要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。目标：求出从初始状态到目标状态的最少步骤和路径（解法）

AStar算法是一种启发式搜索算法，它通过引入启发式函数来评估每个状态的价值。启发式函数是一个估计函数，用来估计从当前状态到目标状态的距离。AStar算法将启发式函数的估计值和已经走过的路径的代价相结合，得到每个状态的价值，从而选择最优的路径。

AStar算法的基本思想是：从初始状态开始，计算每个状态的价值，并选择价值最小的状态作为下一步的目标。在计算状态的价值时，A算法将已经走过的路径的代价和启发式函数的估计值相结合，得到状态的总价值。具体地，A*算法使用以下公式计算状态的总价值：

f(n)=g(n)+h(n)f(n) = g(n) + h(n)

其中，f(n)表示状态n的总价值，g(n)表示从初始状态到状态n的代价，h(n)表示从状态n到目标状态的估计代价。

AStar算法通过遍历状态空间，计算每个状态的总价值，并选择总价值最小的状态作为下一步的目标。如果找到了目标状态，算法就停止搜索，输出解决方案。如果遍历完整个状态空间，仍然没有找到目标状态，算法就停止搜索，输出无解。

AStar算法解决八数码难题的代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import heapq  
  
class Node:  
    def __init__(self, state, parent=None, action=None):  
        self.state = state  
        self.parent = parent  
        self.action = action  
        self.cost = 0  
        self.heuristic = self.calculate_heuristic()  
  
    def calculate_heuristic(self):  
        # 启发式函数：计算当前状态与目标状态的错位数码数量  
        target = [1, 2, 3, 4, 5, 6, 7, 8, 0]  
        return sum(1 for i in range(len(self.state)) if self.state[i] != target[i] and self.state[i] != 0)  
  
    def __lt__(self, other):  
        return self.cost + self.heuristic < other.cost + other.heuristic  
  
    def __str__(self):  
        return f"State: {self.state}, Cost: {self.cost}, Heuristic: {self.heuristic}, Action: {self.action}" 
  
def get_neighbors(node):  
    zero_index = node.state.index(0)  
    zero_row, zero_col = divmod(zero_index, 3)  
    neighbors = []  
    actions = [(-1, 0), (1, 0), (0, -1), (0, 1)]  # 上、下、左、右  
    for action in actions:  
        new_row, new_col = zero_row + action[0], zero_col + action[1]  
        if 0 <= new_row < 3 and 0 <= new_col < 3:  
            new_index = new_row * 3 + new_col  
            new_state = [num for i, num in enumerate(node.state) if i != zero_index]  
            new_state.insert(new_index, 0)  
            neighbors.append(Node(new_state, node, action))  
    return neighbors  
  
def solve_puzzle(initial_state):  
    root = Node(initial_state)  
    frontier = []  
    explored = set()  
    heapq.heappush(frontier, root)  
  
    while frontier:  
        current = heapq.heappop(frontier)  
        if current.state == [2, 8, 3,
                             0, 1, 4, 
                             7, 6, 5]:  
            # 找到目标状态，构建路径  
            path = []  
            while current:  
                path.append((current.action, current.state))  
                current = current.parent  
            return len(path)-1, path[::-1]  # 返回步数和路径（逆序）  
        explored.add(tuple(current.state))  
        for neighbor in get_neighbors(current):  
            if tuple(neighbor.state) not in explored:  
                neighbor.cost = current.cost + 1  
                heapq.heappush(frontier, neighbor)  
    return None, None  # 没有找到解  
  
def print_solution(steps, path):  
    if steps is None:  
        print("没有找到解决方案！")  
        return  
    print(f"最少步骤: {steps}")  
    print("路径:")  
    for action, state in path:  
        print(f"动作: {action}, 状态:")  
        for i in range(3):  
            row = " ".join(str(num) for num in state[i*3:(i+1)*3])  
            print(row)  
        print()  
  
initial_state = [2, 8, 3, 
                 1, 0, 4, 
                 7, 6, 5]  # 初始状态  
steps, path = solve_puzzle(initial_state)  
print_solution(steps, path)

输出如下：

人工智能与专家系统
#HW #Python #BFS #DFS #AStar算法 #α-β剪枝
DUT人工智能与专家系统_HW1
http://horizongazer.github.io/2024/02/15/DUT人工智能与专家系统_HW1/
作者
HorizonGazer
发布于
2024年2月15日
许可协议