完全信息静态博弈的纯策略 / 混合策略nash均衡

纯策略的完全信息静态博弈之Cournot双寡头竞争模型分析

古诺模型（Cournot model）是博弈论中最具有代表性的模型之一，也是是纳什均衡最早的版本。它是法国经济学家古诺（Augustin Cournot）在1938年出版的《财富理论的数学原理研究》一书中最先提出的。而古诺的定义比纳什的定义早了一百多年。从经济学的角度，它的研究价值在于古诺模型是介于两种极端状况完全竞争和垄断之间。在古诺生活的时代，大多数市场都只有少数的厂商经营，所以这个模型在当时是极具现实意义的。随着时间的推移，古诺模型也演变出了各种不同的版本。如果从博弈论的角度分析，有四种情况极具代表性：完全信息静态博弈的古诺模型、不完全信息静态博弈的古诺模型、完全且完美信息动态博弈的古诺模型、无限次重复博弈的古诺模型。这里介绍完全信息静态博弈的古诺模型。

在完全信息博弈的框架下，古诺双寡头竞争模型是研究企业产量竞争的经典案例。市场中仅有两家企业，双方以 产量 为战略变量，以 利润最大化 为目标，最终通过求解纳什均衡得出竞争结果。古诺双寡头模型的纯策略纳什均衡假设两家企业均选择一个确定的产量（而非随机产量）作为策略，且在对方产量给定的情况下，己方产量已无法进一步提高自身利润。

一、模型设定

模型的核心参数与函数定义如下，所有推导基于以下设定展开：

• 产量变量：令q_i ∈ [0, ∞)表示第i个企业的产量（i = 1, 2），即企业1产量为q₁，企业2产量为q₂。

• 成本函数：两家企业具有相同的不变单位成本c（即每生产1单位产品的成本固定为c），因此第i个企业的总成本函数为：C_i(q_i) = q_ic

• 需求函数：市场需求满足线性逆需求函数（价格P关于总产量Q的函数），其中Q = q₁ + q₂为市场总产量，a为需求曲线截距（代表市场最大潜在价格），且满足a > c（确保市场存在有效供给），具体形式为： P = a − (q₁ + q₂)

• 利润函数：第i个企业的利润等于总收益-总成本，总收益为产量×价格，因此利润函数为： π_i(q₁, q₂) = q_i[a − (q₁ + q₂)] − q_ic

二、纳什均衡求解

古诺模型的纳什均衡 (q₁^*, q₂^*) 需满足双方均无动机单独偏离当前产量，即对任意产量 q₁ 和 q₂，均满足：

π₁(q₁^*, q₂^*) ≥ π₁(q₁, q₂^*),  π₂(q₁^*, q₂^*) ≥ π₂(q₁^*, q₂)

1. 求解一阶最优化条件

利润最大化的必要条件是利润函数对自身产量的偏导数为 0（边际利润为 0）。分别对两家企业的利润函数求偏导并令其为 0：

• 企业 1 的一阶条件：

$$ \frac{\partial \pi_1}{\partial q_1} = (a - q_1 - q_2) - q_1 - c = 0 $$

• 企业 2 的一阶条件：

$$ \frac{\partial \pi_2}{\partial q_2} = (a - q_1 - q_2) - q_2 - c = 0 $$

整理上述一阶条件，得到关于产量的线性方程：

$$ \begin{aligned} 2q_1 &= a - q_2 - c \\ 2q_2 &= a - q_1 - c \end{aligned} $$

2. 推导反应函数

反应函数描述给定对方产量时，自身的最优产量。通过整理一阶条件，分别解出 q₁ 和 q₂：

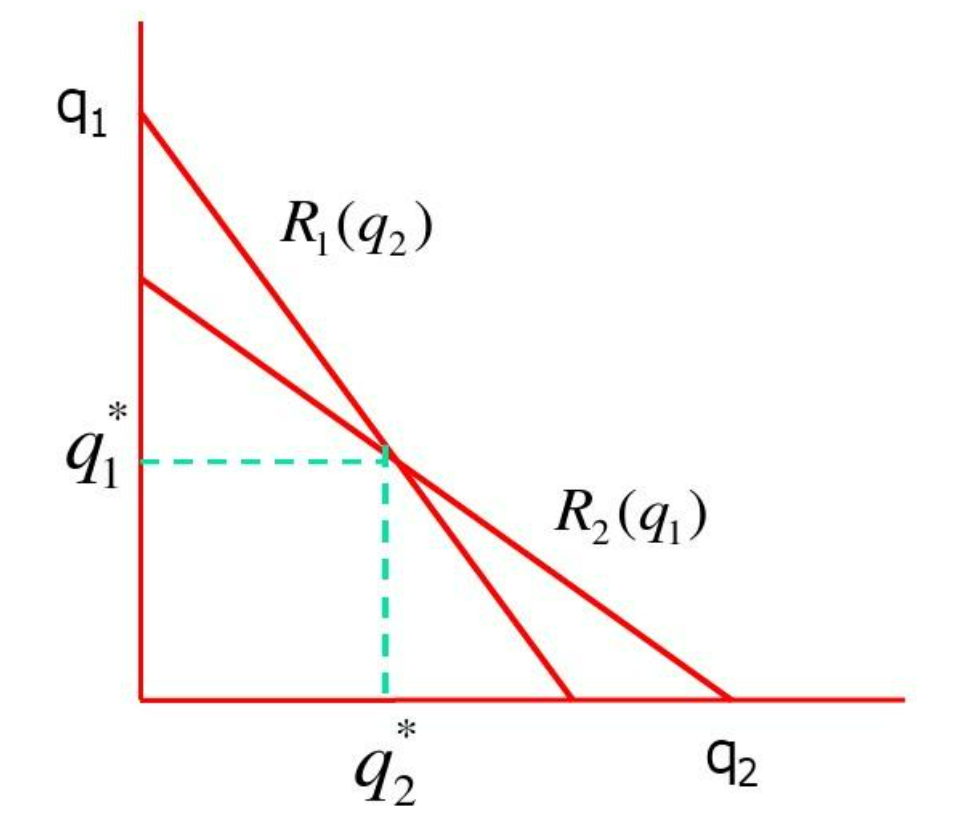
• 企业 1 对企业 2 产量 $ q_2 $ 的反应函数 R₁(q₂)：$$q_1^* = R_1(q_2) = \frac{1}{2}(a - q_2 - c)$$
• 企业 2 对企业 1 产量 $ q_1 $ 的反应函数 R₂(q₁)：$$ q_2^* = R_2(q_1) = \frac{1}{2}(a - q_1 - c) $$

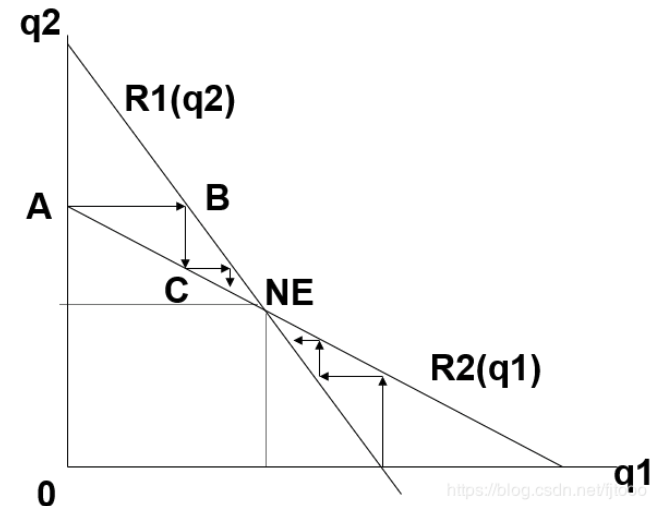
3. 联立求解纳什均衡产量

纳什均衡需同时满足两家企业的反应函数，因此将两个反应函数联立：

$$ \begin{aligned} q_1^* &= \frac{1}{2}(a - q_2^* - c) \\ q_2^* &= \frac{1}{2}(a - q_1^* - c) \end{aligned} $$ 将第二个方程代入第一个方程，展开并整理：

$$ q_1^* = \frac{1}{2}\left[ a - \frac{1}{2}(a - q_1^* - c) - c \right] $$ 最终解得两家企业的纳什均衡产量：

$$ q_1^* = q_2^* = \frac{1}{3}(a - c) $$

4. 计算均衡利润

将均衡产量 $ q_1^* = q_2^* = (a - c) $ 代入利润函数，计算单个企业的均衡利润：

$$ \pi_i(q_1^*, q_2^*) = \frac{1}{3}(a - c) \cdot \left[ a - \left( \frac{1}{3}(a - c) + \frac{1}{3}(a - c) \right) - c \right] $$ 化简后得到单个企业的均衡利润：

$$ \pi_i(q_1^*, q_2^*) = \frac{1}{9}(a - c)^2 $$

三、与垄断情形的比较

为凸显双寡头竞争的结果，引入 垄断模型 作为参照（假设市场由单一企业垄断，成本、需求假设与古诺模型一致）。

1. 垄断企业的利润最大化求解

• 垄断利润函数：垄断企业的总产量即为市场产量 Q​，利润函数为：

max_Qπ = Q(a − Q − c)

• 一阶条件：对利润函数求导并令其为 0，得：

$$ \frac{\partial \pi}{\partial Q} = a - 2Q - c = 0 $$

• 垄断均衡产量：

$$ Q_{\text{monopoly}}^* = \frac{1}{2}(a - c) $$

• 垄断均衡利润：将 $ Q_{}^* $ 代入利润函数，得：

$$ \pi_{\text{monopoly}}^* = \frac{1}{4}(a - c)^2 $$

2.核心指标对比

指标	垄断模型（单一企业）	古诺双寡头模型（两家企业）	结论
市场总产量	$$ Q_{\text{monopoly}}^* = \frac{1}{2}(a - c) $$	$$ Q_{\text{Cournot}}^* = \frac{2}{3}(a - c) $$	垄断总产量 < 寡头总产量
市场总利润	$$ \pi_{\text{monopoly}}^* = \frac{1}{4}(a - c)^2 $$	$$ \pi_{\text{Cournot}}^* = \frac{2}{9}(a - c)^2 $$	垄断总利润 > 寡头总利润

四、结论

1. 产量层面：双寡头竞争下的市场总产量（$\frac{2}{3}(a - c)$）高于垄断总产量（$\frac{1}{2}(a - c)$），表明企业间的产量竞争会推动市场供给增加。

2. 利润层面：双寡头竞争下的市场总利润（$\frac{2}{9}(a - c)^2$）低于垄断利润（ $\frac{1}{4}(a - c)^2$），表明竞争会压缩企业的利润空间。

综上，古诺双寡头模型中，企业的产量竞争最终导致 总产量上升、总利润下降，这一结果体现了市场竞争对资源配置和企业收益的核心影响。

混合策略的完全信息静态博弈之小偷与守卫

从经济学角度上讲，对于理性的人，犯罪成本高于犯罪收益，自然就不会去犯罪。所以简单回答就是，违法成本变高会减少犯罪。使违法成本变高有很多方法，最直接最常见的就是严打，即加大对犯罪的处罚力度。小偷-守卫博弈有助于我们对这些方面的思考，该博弈在双方采用纯策略的情况下不存在纳什均衡，但在双方采用混合策略的情况下存在纳什均衡，且双方都没有动机偏离该纳什均衡。

一、模型设定

小偷 - 守卫博弈是博弈论中研究混合策略纳什均衡与激励机制的经典模型，其核心参与主体为 守卫 与 小偷，二者均为追求自身效用最大化的理性决策者。守卫的策略空间包含 睡眠（失职）与 值守（尽职），小偷的策略空间包含 盗窃 与 不盗窃，不同策略组合下的效用设定如下：

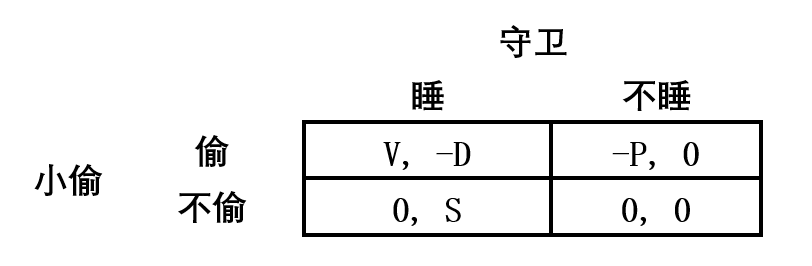
1. 若守卫选择 睡眠、小偷选择 盗窃：小偷获得正效用V（盗窃收益），守卫获得负效用−D（失职惩罚）；

2. 若守卫选择 值守、小偷选择 盗窃：小偷获得负效用−P（盗窃惩罚），守卫效用为 0（尽职无额外收益也无损失）；

3. 若守卫选择 睡眠、小偷选择 不盗窃：守卫获得正效用S（偷懒收益），小偷效用为 0（无盗窃行为则无收益损失）；

4. 若守卫选择 值守、小偷选择 不盗窃：双方效用均为 0（守卫尽职无收益，小偷不行动无收益）。

该博弈不存在纯策略纳什均衡 —— 即不存在某一固定策略组合，使得双方均无动机单独改变策略。因此，需通过求解混合策略纳什均衡，分析双方的最优概率选择。

二、混合策略纳什均衡的求解

混合策略纳什均衡的核心逻辑是：参与者以特定概率随机选择不同策略，使得对方无论选择何种纯策略，期望得益均相等，从而双方均无动机偏离该概率分布。

1.小偷混合策略概率的确定

设小偷选择 盗窃 的概率为p_t，则选择 不盗窃 的概率为1 − p_t。为使守卫在 睡眠 与 值守 两种策略下的期望得益相等，需满足以下等式： −D × p_t + S × (1 − p_t) = 0 × p_t + 0 × (1 − p_t) 化简后求解得小偷选择 盗窃 的最优概率： $$ p_t^* = \frac{S}{D + S} $$ 从经济意义看，若守卫 睡眠 的收益S越高（偷懒成本越低），或守卫 失职 的惩罚D越低，小偷选择 盗窃 的概率p_t^*会越高；反之则越低。当小偷以p_t^*概率 盗窃 时，守卫 睡眠 与 值守 的期望得益均为 0，无论选择纯策略还是混合策略，期望收益均无差异，从而失去改变策略的动机。

2.守卫混合策略概率的确定

设守卫选择 睡眠 的概率为p_g，则选择 值守 的概率为1 − p_g。同理，为使小偷在 盗窃 与 不盗窃 两种策略下的期望得益相等，需满足：

代入效用值可得： V × p_g + (−P) × (1 − p_g) = 0 × p_g + 0 × (1 − p_g) 化简后求解得守卫选择 睡眠 的最优概率： $$ p_g^* = \frac{P}{V + P} $$ 该结果表明，若小偷盗窃的收益V越高（仓库物品越重要），或小偷盗窃的惩罚P越高，守卫选择睡眠的概率p_g^*会越低（即更倾向于值守）；反之则越高。当守卫以p_g^*概率睡眠时，小偷盗窃与不盗窃的期望得益均为0，同样无动机改变策略。

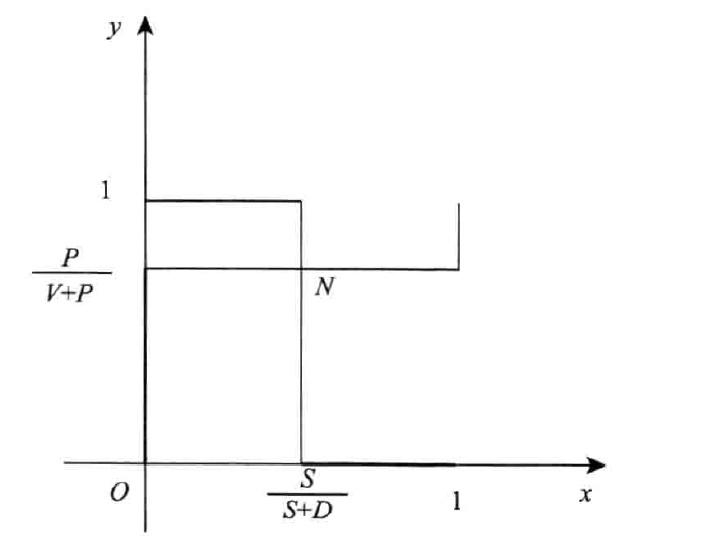
综上，该博弈唯一的混合策略纳什均衡为：小偷以$p_t^*=\frac{S}{D+S}$概率盗窃、1 − p_t^*概率不盗窃；守卫以$p_g^*=\frac{P}{V+P}$概率睡眠、1 − p_g^*概率值守。

三、激励的悖论

基于混合策略纳什均衡的分析，可推导出激励的悖论——即政策制定者为抑制犯罪而采取的激励措施，可能产生与目标相悖的长期效果，具体表现为以下两种情形：

1.加重对小偷的惩罚（提高P）

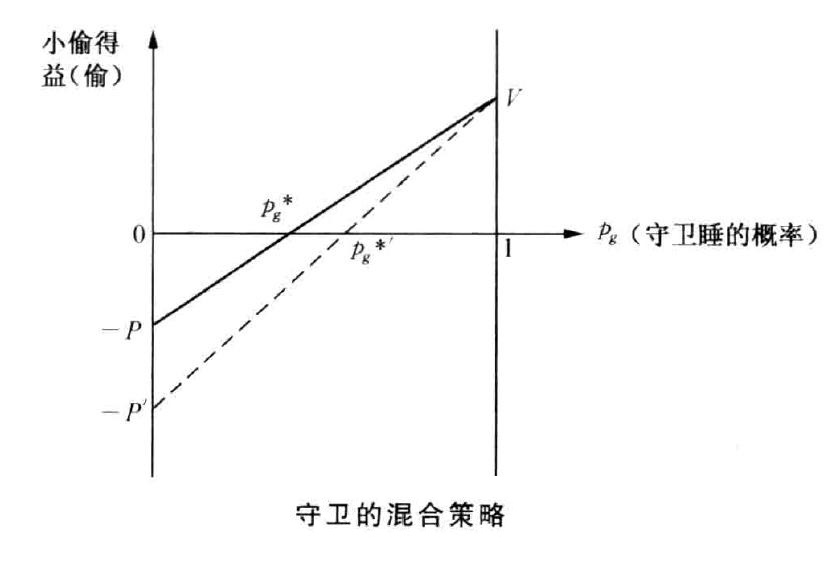
当政策加重对小偷的盗窃惩罚（P增大至P′）时，短期来看，若守卫仍维持原均衡概率p_g^*，小偷盗窃的期望得益会变为负值，小偷会暂时停止盗窃行为。但长期中，小偷盗窃频率的下降会降低守卫值守的必要性，守卫会逐渐提高睡眠的概率，直至达到新的均衡概率$p_g'=\frac{P'}{V+P'}$。此时，小偷盗窃的期望得益重新恢复为0，会再次选择混合策略（以$p_t^*=\frac{S}{D+S}$概率盗窃）。

最终结论：加重对小偷的惩罚仅能抑制短期盗窃率，对长期盗窃率无影响；其长期作用是提高守卫的偷懒概率，而非降低犯罪发生率。

2.加重对守卫的惩罚（提高D）

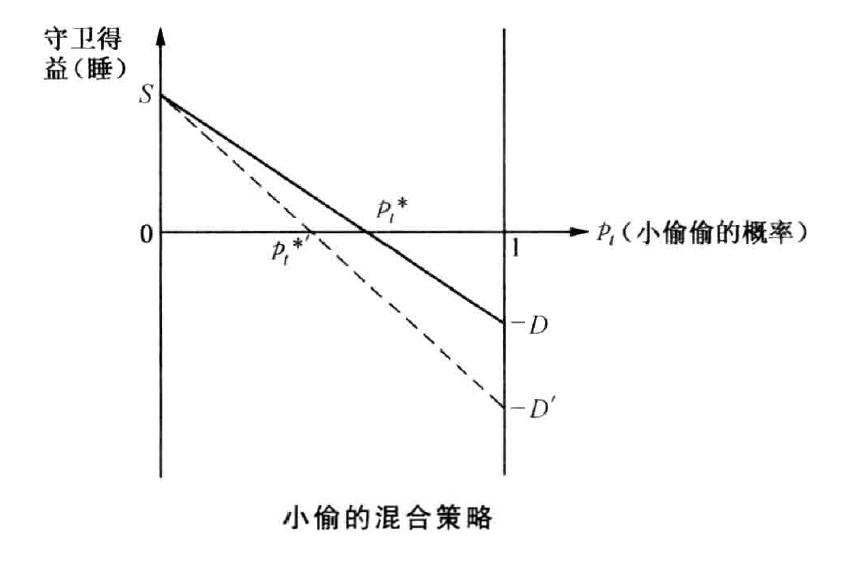
当政策加重对守卫的失职惩罚（D增大至D′）时，短期来看，若小偷仍维持原均衡概率p_t^*，守卫睡眠的期望得益会变为负值，守卫会暂时选择值守。但长期中，守卫的尽职会增加小偷盗窃的风险，小偷会逐渐降低盗窃的概率，直至达到新的均衡概率$p_t'=\frac{S}{D'+S}$。此时，守卫睡眠与值守的期望得益重新恢复为0，会再次选择混合策略（以$p_g^*=\frac{P}{V+P}$概率睡眠）。

最终结论：加重对守卫的惩罚仅能短期提升守卫的尽职程度，长期中无法改变守卫的勤勉概率；但其长期作用是降低盗窃事件的发生率，与政策抑制犯罪的目标一致。

四、模型的启示

针对现实中参与者难以主动选择均衡概率的疑问，纳什提出的群体行为解释可有效回应：混合策略的概率分布并非个体主动计算的结果，而是大量同类参与者在长期博弈中形成的策略选择频率。例如，小偷盗窃概率p_t^*可理解为某一地区偷盗案件的发生频率，守卫睡眠概率p_g^*可理解为该地区守卫中偷懒者的比例。这种频率的稳定性即构成群体层面的混合策略均衡，无需个体具备复杂的概率计算能力，因此更贴合现实场景。

五、总结

小偷-守卫博弈作为博弈论的经典模型，其核心价值在于揭示了混合策略纳什均衡的存在性与激励悖论的现实意义。模型证明，理性参与者的策略选择不仅取决于自身的收益与成本，还受对方策略概率的影响；而政策制定需突破单纯加重违法惩罚的惯性思维，通过优化对监管者的激励机制，实现长期治理目标。该模型的分析逻辑可延伸至安全生产监管、食品安全督查等多个领域，为解决现实中的监管者-违规者博弈问题提供重要的理论参考。

参考

https://leilie.top/2023-07-16/Study-Cournot-Model

https://www.cnblogs.com/haohai9309/p/17833572.html

https://www.cnblogs.com/haohai9309/p/17841008.html

---

碎碎念：本人对象于10月14日在小红书直播间抽中香酥鱼皮一包，望周知（已求婚版）