神经网络模型FGSM攻击实践

本实践作业旨在通过实验验证深度神经网络模型对对抗攻击的脆弱性。本实验针对图像分类任务，实现了快速梯度符号法（FGSM）对抗攻击算法，并在CIFAR-10数据集上进行了系统性测试。实验结果表明，即使是微小的、人类难以察觉的扰动，也能导致神经网络模型的预测性能显著下降。

实验目标

理解对抗样本的基本概念和生成原理
掌握FGSM攻击方法
评估对抗样本对模型性能的影响

理论基础

对抗攻击定义

给定一个训练好的神经网络模型 f_θ(x)，其中 θ 表示模型参数，x 为输入样本，y 为真实标签。对抗攻击的目标是找到一个扰动 δ，使得：

f_θ(x + δ) ≠ y, 且 ||δ||_p ≤ ϵ

其中 ϵ 是扰动的最大允许幅度，||⋅||_p 表示 L_p 范数。

好，我们来简单地介绍一下范数。数学中，范数是一个函数，它为线性空间（例如向量空间）中的每个向量赋予一个非负的实数值。你可以将它理解为 “长度” 概念的推广。

对于一个向量 x，其范数通常表示为 ||x||。它必须满足以下三个性质：

非负性：||x|| ≥ 0，且 ||x|| = 0 当且仅当 x 是零向量。
齐次性：对于任意标量 α，有 ||αx|| = |α| · ||x||。
三角不等式：对于任意向量 x, y，有 ||x + y|| ≤ ||x|| + ||y||。

最常见的范数族是 Lₚ 范数（读作“L-p范数”）。对于一个 n 维向量 x = (x₁, x₂, …, xₙ)，其 Lₚ 范数定义为：

||x||_p = (|x₁|^p + |x₂|^p + … + |xₙ|^p)^1/p

通过改变 p 的值，我们可以得到不同的范数。

范数名称	符号	计算公式 (对于向量 x ∈ Rⁿ)	几何意义 / 特点	主要应用场景
L₁ 范数 (曼哈顿范数)	‖x‖₁	‖x‖₁ = \|x₁\| + \|x₂\| + … + \|xₙ\|	各维度坐标绝对值的和。想象在曼哈顿街区（网格状道路）上行走的总距离。	特征选择、稀疏编码、压缩感知。因为它倾向于产生稀疏解（许多分量为零）。
L₂ 范数 (欧几里得范数)	‖x‖₂	‖x‖₂ = √(x₁² + x₂² + … + xₙ²)	从原点到向量点的直线距离。这是我们最熟悉的“长度”概念。	机器学习中最常用，如： • 正则化 (岭回归) • 度量距离 (KNN, K-Means) • 模型评估 (均方误差根)
Lₚ 范数	‖x‖ₚ	‖x‖ₚ = ( \|x₁\|ᵖ + \|x₂\|ᵖ + … + \|xₙ\|ᵖ )^1/p	p 值不同，等值线（范数相等的点集）形状不同。p=1是菱形，p=2是圆形，p>2逐渐向矩形过渡。	作为 L₁ 和 L₂ 的推广，在特定优化问题中使用。
L∞ 范数 (极大范数 / 切比雪夫范数)	‖x‖∞	‖x‖∞ = max(\|x₁\|, \|x₂\|, …, \|xₙ\|)	所有维度坐标绝对值的最大值。	误差分析，当最差情况的误差（最大误差）是关注重点时。例如，在制造中保证零件的最大公差。
L₀ “范数”	‖x‖₀	向量中非零元素的个数。	注意：L₀ “范数”实际上不满足范数的齐次性，因此不是一个真正的范数。但它非常重要。	衡量向量的稀疏度。在理想情况下用于稀疏优化，但由于其非凸性，常被 L₁ 范数替代。

FGSM算法原理

快速梯度符号法（Fast Gradient Sign Method, FGSM）是一种基于梯度的单步攻击方法，其更新公式为：

x_adv = x + ϵ ⋅ sign(∇_xℒ(f_θ(x), y))

其中 ℒ 是损失函数，sign 是符号函数，ϵ 控制扰动幅度。

攻击者需要知道目标模型的结构、参数和梯度，并且仅通过一次梯度计算生成对抗样本（无需迭代），沿梯度符号方向添加扰动，最大化损失函数，迫使模型预测错误。步骤如下

计算梯度：对输入 x 计算损失函数 L 的梯度： ∇_xL
生成扰动：根据梯度符号和扰动幅度 ϵ，构造扰动： δ = ϵ ⋅ sign(∇_xL)
生成对抗样本：将扰动 δ 加到原始输入 x 上： x_adv = x + δ
裁剪输入：确保对抗样本 x_adv 的像素值仍在合法范围内（如 [0, 1]）： x_adv = clip(x_adv, 0, 1)

CIFAR-10

CIFAR-10 是计算机视觉领域经典的图像分类基准数据集，由加拿大高级研究所（CIFAR）发布，因数据规模适中、标注清晰，成为入门级图像识别任务的核心训练与测试数据，广泛用于卷积神经网络（CNN）等模型的基础研发。

它的样本设计聚焦 “低门槛、高通用性”，所有图像均为 32×32 像素的彩色图，包含 RGB 三个颜色通道，单张图像数据量小，能大幅降低模型训练的硬件门槛和时间成本。类别上则涵盖 10 个完全互斥的日常物体类别，且每个类别样本数量均衡，具体包括鸟、猫、鹿、狗、青蛙等动物类，以及飞机、汽车、船、卡车等交通工具类，这种划分既贴近现实场景，又避免了类别混淆度过高的问题，适合验证模型的基础分类能力，整个数据集共包含 60000 张无重复或重叠的图像。

为适配 “训练 - 测试” 的标准机器学习流程，CIFAR-10 的数据集划分清晰且固定，无需额外处理。其中训练集共 50000 张图像，每个类别各 5000 张，占总数据量的 83.3%，主要用于模型的参数学习和迭代优化；测试集则包含 10000 张图像，每个类别各 1000 张，占总数据量的 16.7%，专门用于独立评估模型在 “未见过的数据” 上的泛化能力，避免模型出现过拟合问题。同时，每张图像都自带唯一的类别标签，标签与图像一一对应，无需用户额外标注，可直接用于监督学习任务，大幅降低了数据预处理的复杂度。

实验设计

实验环境

深度学习框架: PyTorch 2.5.1+cu121

Python版本: 3.10.0

硬件环境: NVIDIA GeForce RTX 4060

数据集: CIFAR-10

模型架构: 自定义并训练的ResNet-20

实验步骤

ResNet-20 模型构建与训练：1）设计适配 CIFAR-10（32×32 彩色图）的 ResNet-20 网络，含残差块与多层卷积架构。2）用随机裁剪、水平翻转做数据增强，SGD 优化器 + 多步学习率衰减策略，训练 200 个 epoch。3）保存训练完成的模型参数，为后续实验提供基础模型。
模型基础分类能力验证：1）从 CIFAR-10 测试集随机采样批次数据。2）可视化对比 “模型预测标签” 与 “样本真实标签”，确认模型基础分类性能。
FGSM 对抗攻击实现与测试：1）开发两种攻击：有目标 FGSM（误导至指定错误类别）、无目标 FGSM（仅需误分类）。2）以 epsilon（0.001-1）为变量，测试两种攻击在 CIFAR-10 各类别的成功率，评估模型鲁棒性。
攻击效果可视化分析：1）对比展示原始样本与对抗样本的视觉差异。2）记录攻击前后模型预测结果变化，用条形图统计不同 epsilon 下的类别攻击成功率。

实验步骤与结果分析

环境配置和初始化

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
import random
plt.rcParams['font.sans-serif'] = ['Noto Sans SC', 'DejaVu Sans', 'Arial']
plt.rcParams['axes.unicode_minus'] = False
torch.cuda.is_available()

NVIDIA GeForce RTX 4060，PyTorch 2.5.1+cu121

ResNet-20模型架构设计

class BasicBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride=1, downsample=None):
        super(BasicBlock, self).__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1, bias=False)
        self.bn1   = nn.BatchNorm2d(out_channels)
        self.relu  = nn.ReLU(inplace=True)
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1, bias=False)
        self.bn2   = nn.BatchNorm2d(out_channels)
        self.downsample = downsample

    def forward(self, x):
        identity = x
        out      = self.conv1(x)
        out      = self.bn1(out)
        out      = self.relu(out)
        out      = self.conv2(out)
        out      = self.bn2(out)
        if self.downsample is not None:
            identity = self.downsample(x)
        out  += identity
        out   = self.relu(out)
        return out

class ResNet(nn.Module):
    def __init__(self, block, layers, num_classes=10):
        super(ResNet, self).__init__()
        self.in_channels = 16
        self.conv   = nn.Conv2d(3, 16, kernel_size=3, padding=1, bias=False)
        self.bn     = nn.BatchNorm2d(16)
        self.relu   = nn.ReLU(inplace=True)
        self.layer1 = self._make_layer(block, 16,  layers[0])
        self.layer2 = self._make_layer(block, 32,  layers[1], stride=2)
        self.layer3 = self._make_layer(block, 64,  layers[2], stride=2)
        self.avgpool= nn.AdaptiveAvgPool2d((1,1))
        self.fc     = nn.Linear(64, num_classes)

    def _make_layer(self, block, out_channels, blocks, stride=1):
        downsample = None
        if stride !=1 or self.in_channels != out_channels:
            downsample = nn.Sequential(
                nn.Conv2d(self.in_channels, out_channels, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(out_channels)
            )
        layers = []
        layers.append(block(self.in_channels, out_channels, stride, downsample))
        self.in_channels = out_channels
        for _ in range(1, blocks):
            layers.append(block(out_channels, out_channels))
        return nn.Sequential(*layers)

    def forward(self, x):
        out = self.conv(x)
        out = self.bn(out)
        out = self.relu(out)
        out = self.layer1(out)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.avgpool(out)
        out = torch.flatten(out, 1)
        out = self.fc(out)
        return out

def resnet20():
    return ResNet(BasicBlock, [3, 3, 3])

该部分实现了经典的ResNet-20深度神经网络。通过定义BasicBlock基础残差块，构建了包含两个卷积层、批归一化和跳跃连接的核心组件。ResNet主类在此基础上组织了完整的网络结构，包含初始卷积层、三个残差层（分别包含3个残差块）、全局平均池化和最终分类层。这种设计有效解决了深度网络中的梯度消失问题，使模型能够学习更加复杂的特征表示，为CIFAR-10图像分类任务提供了强大的特征提取能力。

数据预处理

# 定义设备
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 数据预处理
transform_train = transforms.Compose([
    transforms.RandomCrop(32, padding=4),
    transforms.RandomHorizontalFlip(),
    transforms.ToTensor(),
])

transform_test = transforms.Compose([
    transforms.ToTensor(),
])

# 加载CIFAR10数据集
train_dataset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform_train)
test_dataset  = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform_test)

train_loader  = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=128, shuffle=True)
test_loader   = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=100, shuffle=False)

针对CIFAR-10数据集的特点，设计了完整的数据处理流程。训练阶段采用随机裁剪和水平翻转等数据增强技术，增加数据的多样性以提高模型泛化能力。测试阶段则保持简单的张量转换。通过DataLoader实现了数据的批量加载，训练批次设为128，测试批次设为100，平衡了内存使用和训练效率。这套数据处理方案为模型训练提供了高质量、标准化的输入数据。

模型训练

定义超参数

model = resnet20().to(device)

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1, momentum=0.9, weight_decay=5e-4) # 使用SGD

# 学习率调整策略
scheduler = optim.lr_scheduler.MultiStepLR(optimizer, milestones=[100, 150], gamma=0.1)

设备选择：GPU（如果可用）或CPU。
损失函数：交叉熵损失。
优化器：SGD，学习率0.1，动量0.9，权重衰减5e-4。
学习率调整：在第100和150个epoch时将学习率乘以0.1。

开始200轮迭代

# CIFAR-10 类别标签
class_names = ['飞机', '汽车', '鸟', '猫', '鹿', '狗', '青蛙', '马', '船', '卡车']
num_epochs = 200

for epoch in range(num_epochs):
    model.train()
    running_loss = 0.0
    for i, (images, labels) in enumerate(train_loader):
        images = images.to(device)
        labels = labels.to(device)

        # 前向传播
        outputs = model(images)
        loss = criterion(outputs, labels)

        # 反向传播
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        running_loss += loss.item()

    scheduler.step()

    # 每10个epoch打印一次训练损失和测试准确率
    if (epoch+1) % 10 == 0:
        model.eval()
        correct = 0
        total = 0
        with torch.no_grad():
            for images, labels in test_loader:
                images = images.to(device)
                labels = labels.to(device)
                outputs = model(images)
                _, predicted = torch.max(outputs.data, 1)
                total += labels.size(0)
                correct += (predicted == labels).sum().item()
        print('Epoch [{}/{}], Loss: {:.4f}, Test Accuracy: {:.2f}%'
              .format(epoch+1, num_epochs, running_loss/len(train_loader), 100 * correct / total))
        # 保存模型
torch.save(model.state_dict(), f'model_rensnet.pth')

Epoch [10/200], Loss: 0.5053, Test Accuracy: 67.28% Epoch [20/200], Loss: 0.4733, Test Accuracy: 77.29% Epoch [30/200], Loss: 0.4607, Test Accuracy: 74.71% Epoch [40/200], Loss: 0.4388, Test Accuracy: 80.89% Epoch [180/200], Loss: 0.0277, Test Accuracy: 92.64% Epoch [190/200], Loss: 0.0258, Test Accuracy: 92.65% Epoch [200/200], Loss: 0.0230, Test Accuracy: 92.79%

进行200个epoch，每个epoch计算训练损失，并在每10个epoch后计算测试准确率。200epoch后Loss: 0.0230, Test Accuracy: 92.79%，基本收敛，还可继续迭代，但这里选择保存模型进行下一步。

测试集验证

# 加载模型权重
# CIFAR-10 类别标签
class_names = ['飞机', '汽车', '鸟', '猫', '鹿', '狗', '青蛙', '马', '船', '卡车']
state_dict = torch.load('model_rensnet.pth')
model.load_state_dict(state_dict)
def imshow(img):
    # img = img / 2 + 0.5  
    img = img.detach().cpu()
    npimg = img.numpy()
    # plt.imshow(npimg)
    plt.imshow(np.transpose(npimg, (1, 2, 0)))


# 可视化模型在测试集上的预测结果
def visualize_predictions(model, test_loader, device):
    model.eval()
    dataiter = iter(test_loader)
    images, labels = next(dataiter)
    images, labels = images.to(device), labels.to(device)

    # 获取模型的预测结果
    outputs = model(images)
    _, predicted = torch.max(outputs, 1)

    # 将图像转换为CPU格式，以便显示
    images = images.cpu()
    predicted = predicted.cpu()
    labels = labels.cpu()

    # 展示4x4的图像及其预测标签
    plt.figure(figsize=(8, 8))
    for idx in range(16):
        plt.subplot(4, 4, idx + 1)
        imshow(images[idx])
        plt.title(f"Pred: {predicted[idx].item()}, True: {labels[idx].item()}")
        plt.axis('off')

    plt.tight_layout()
    plt.show()

# 获取任意一个批次
def get_random_batch(test_loader):
    dataiter = iter(test_loader)
    # 随机选择一个批次索引
    batch_idx = random.randint(0, len(test_loader) - 1)
    for idx, (images, labels) in enumerate(dataiter):
        if idx == batch_idx:
            return images, labels
visualize_predictions(model, test_loader, device)

测试集中选取16张图片，分类预测准确度15/16。下一步进行FGSM攻击。

FGSM攻击函数定义

# FGSM 有目标攻击
def fgsm_targeted_attack(model, device, data, target_labels, epsilon):
    """
    FGSM 有目标攻击 - 使模型将输入误分类为指定的目标类别
    
    参数:
        model: 目标模型
        device: 设备 (CPU/GPU)
        data: 输入数据 (batch_size, channels, height, width)
        target_labels: 目标标签 (batch_size)
        epsilon: 扰动强度
    
    返回:
        perturbed_data: 添加扰动后的数据
    """
    # 确保模型处于评估模式
    model.eval()
    
    # 设置需要计算梯度
    data = data.clone().detach().to(device)
    data.requires_grad = True
    target_labels = target_labels.to(device)
    
    # 前向传播
    outputs = model(data)
    
    # 计算损失 - 有目标攻击要最大化目标类别的概率
    criterion = nn.CrossEntropyLoss()
    loss = criterion(outputs, target_labels)
    
    # 反向传播
    model.zero_grad()
    loss.backward()
    
    # 获取输入数据的梯度
    data_grad = data.grad.data
    
    # 生成扰动 - 有目标攻击是朝着目标类别的方向
    perturbation = -epsilon * data_grad.sign()
    
    # 生成对抗样本
    perturbed_data = data + perturbation
    
    # 裁剪到有效范围 [0, 1]
    perturbed_data = torch.clamp(perturbed_data, 0, 1)
    
    return perturbed_data

# FGSM 无目标攻击
def fgsm_untargeted_attack(model, device, data, labels, epsilon):
    """
    FGSM 无目标攻击 - 使模型对输入产生错误分类
    
    参数:
        model: 目标模型
        device: 设备 (CPU/GPU)
        data: 输入数据 (batch_size, channels, height, width)
        labels: 真实标签 (batch_size)
        epsilon: 扰动强度
    
    返回:
        perturbed_data: 添加扰动后的数据
    """
    # 确保模型处于评估模式
    model.eval()
    
    # 设置需要计算梯度
    data = data.clone().detach().to(device)
    data.requires_grad = True
    labels = labels.to(device)
    
    # 前向传播
    outputs = model(data)
    
    # 计算损失 - 无目标攻击要最小化真实类别的概率
    criterion = nn.CrossEntropyLoss()
    loss = criterion(outputs, labels)
    
    # 反向传播
    model.zero_grad()
    loss.backward()
    
    # 获取输入数据的梯度
    data_grad = data.grad.data
    
    # 生成扰动 - 无目标攻击是朝着损失增加的方向
    perturbation = epsilon * data_grad.sign()
    
    # 生成对抗样本
    perturbed_data = data + perturbation
    
    # 裁剪到有效范围 [0, 1]
    perturbed_data = torch.clamp(perturbed_data, 0, 1)
    
    return perturbed_data

有目标攻击通过计算损失函数对输入数据的梯度，沿着使模型分类到指定目标类别的负梯度方向添加扰动。

无目标攻击则沿着正梯度方向诱导任意形式的误分类。两种攻击方法都通过epsilon参数精确控制扰动强度，并利用sign函数确保扰动方向的一致性。

不同扰动强度下的攻击效果

针对CIFAR-10的10个类别系统测试了从0.001到1.0共7个不同扰动强度下的攻击效果，每个类别采样1000个初始分类正确的样本进行统计，确保了实验结果的可靠性和可重复性。

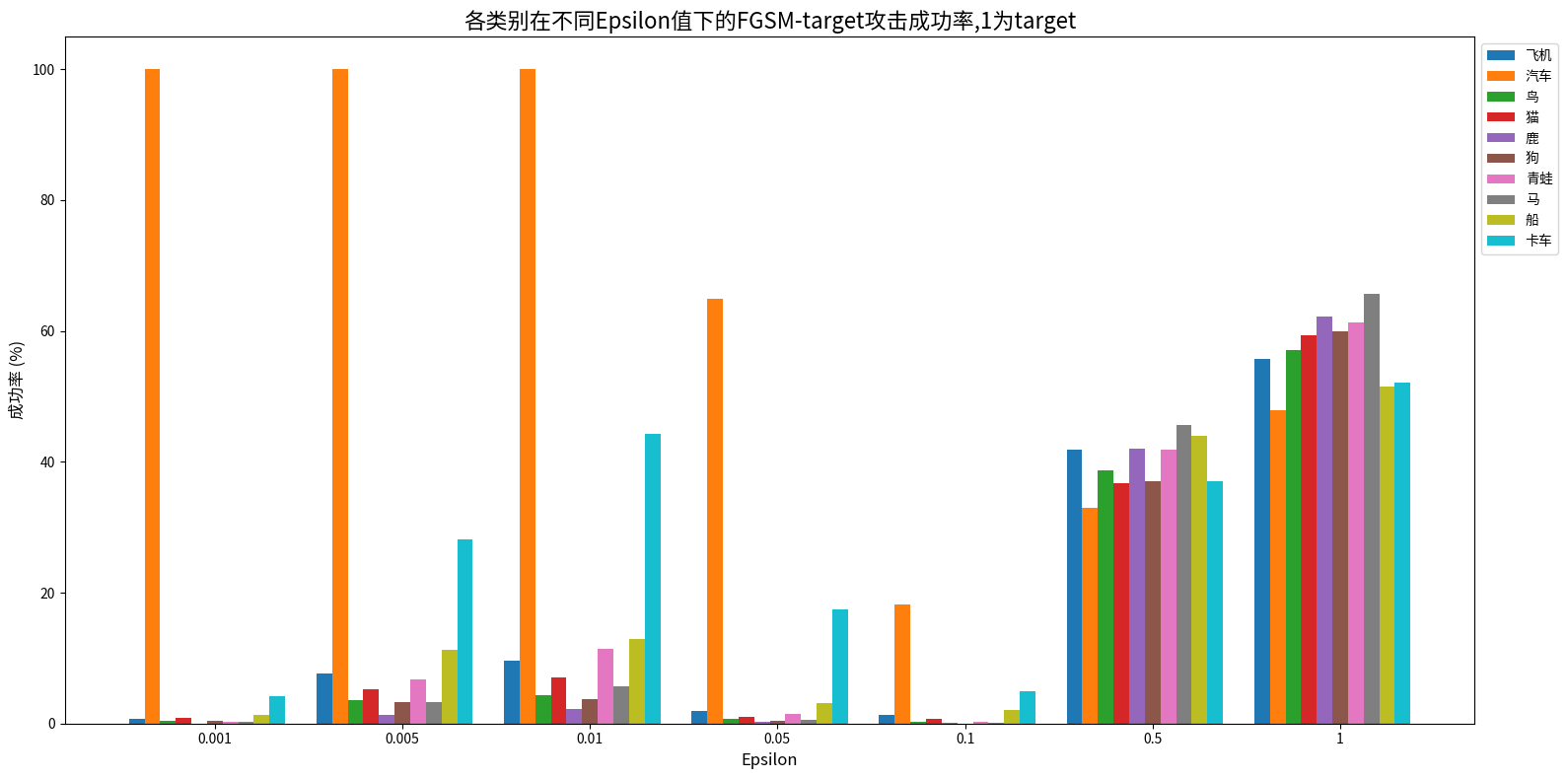
FGSM有目标攻击

# target attack
epsilon_list = [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1]  # 可根据需要调整
target_label = 1  # 例如，目标攻击的类别为"汽车" (类别编号为1)


results_target = {class_name: [] for class_name in class_names}

# 遍历每个类别进行攻击
for i in range(10):  # CIFAR-10 共有10个类别
    print(f"类别: {class_names[i]}，类别编号: {i}")

    # 设置目标标签为某一类别
    target_label_tensor = torch.tensor([target_label]).to(device)  # 将目标设置为“汽车”

    for epsilon in epsilon_list:
        # 统计攻击成功率
        success = 0
        total = 0

        for data, label in test_loader:
            data, label = data.to(device), label.to(device)

            # 初始预测
            output = model(data)
            init_pred = output.max(1, keepdim=True)[1]

            # 仅对属于当前测试类别且初始预测正确的样本进行攻击
            correct_indices = (init_pred.squeeze() == label) & (label == i)
            if correct_indices.sum().item() == 0:
                continue

            data = data[correct_indices]
            label = label[correct_indices]

            # 创建目标标签张量
            target_labels = torch.full_like(label, target_label_tensor.item())

            # 对每个样本进行FGSM目标攻击
            perturbed_data = fgsm_targeted_attack(model, device, data, target_labels, epsilon)

            # 测试对抗样本
            output = model(perturbed_data)
            final_pred = output.max(1, keepdim=True)[1]

            # 统计成功将模型误导到目标类别的样本数量
            success += (final_pred.squeeze() == target_label_tensor).sum().item()
            total += data.size(0)

            # 控制测试样本数量（1000张图片）
            if total >= 1000:
                break
        success_rate = 100 * success / total if total > 0 else 0
        print(f"epsilon = {epsilon:.3f}, 目标攻击成功率：{100 * success / total:.2f}%")
        results_target[class_names[i]].append(success_rate)
    print("\n")

类别: 飞机，类别编号: 0 epsilon = 0.001, 目标攻击成功率：0.74% epsilon = 0.005, 目标攻击成功率：7.64% epsilon = 0.010, 目标攻击成功率：9.66% epsilon = 0.050, 目标攻击成功率：1.91% epsilon = 0.100, 目标攻击成功率：1.38% epsilon = 0.500, 目标攻击成功率：41.93% epsilon = 1.000, 目标攻击成功率：55.73%

类别: 汽车，类别编号: 1 epsilon = 0.001, 目标攻击成功率：100.00% epsilon = 0.005, 目标攻击成功率：100.00% epsilon = 0.010, 目标攻击成功率：100.00% epsilon = 0.050, 目标攻击成功率：64.96% epsilon = 0.100, 目标攻击成功率：18.20% epsilon = 0.500, 目标攻击成功率：32.95% epsilon = 1.000, 目标攻击成功率：47.91%

类别: 鸟，类别编号: 2 epsilon = 0.001, 目标攻击成功率：0.44% epsilon = 0.005, 目标攻击成功率：3.55% epsilon = 0.010, 目标攻击成功率：4.33% epsilon = 0.050, 目标攻击成功率：0.67% epsilon = 0.100, 目标攻击成功率：0.22% epsilon = 0.500, 目标攻击成功率：38.73% epsilon = 1.000, 目标攻击成功率：57.16%

类别: 猫，类别编号: 3 epsilon = 0.001, 目标攻击成功率：0.83% epsilon = 0.005, 目标攻击成功率：5.21% epsilon = 0.010, 目标攻击成功率：6.98% epsilon = 0.050, 目标攻击成功率：0.95% epsilon = 0.100, 目标攻击成功率：0.71% epsilon = 0.500, 目标攻击成功率：36.69% epsilon = 1.000, 目标攻击成功率：59.41%

类别: 鹿，类别编号: 4 epsilon = 0.001, 目标攻击成功率：0.00% epsilon = 0.005, 目标攻击成功率：1.37% epsilon = 0.010, 目标攻击成功率：2.22% epsilon = 0.050, 目标攻击成功率：0.21% epsilon = 0.100, 目标攻击成功率：0.11% epsilon = 0.500, 目标攻击成功率：42.07% epsilon = 1.000, 目标攻击成功率：62.26%

类别: 狗，类别编号: 5 epsilon = 0.001, 目标攻击成功率：0.34% epsilon = 0.005, 目标攻击成功率：3.20% epsilon = 0.010, 目标攻击成功率：3.66% epsilon = 0.050, 目标攻击成功率：0.34% epsilon = 0.100, 目标攻击成功率：0.00% epsilon = 0.500, 目标攻击成功率：37.03% epsilon = 1.000, 目标攻击成功率：60.00%

类别: 青蛙，类别编号: 6 epsilon = 0.001, 目标攻击成功率：0.21% epsilon = 0.005, 目标攻击成功率：6.76% epsilon = 0.010, 目标攻击成功率：11.40% epsilon = 0.050, 目标攻击成功率：1.48% epsilon = 0.100, 目标攻击成功率：0.32% epsilon = 0.500, 目标攻击成功率：41.82% epsilon = 1.000, 目标攻击成功率：61.35%

类别: 马，类别编号: 7 epsilon = 0.001, 目标攻击成功率：0.21% epsilon = 0.005, 目标攻击成功率：3.28% epsilon = 0.010, 目标攻击成功率：5.71% epsilon = 0.050, 目标攻击成功率：0.63% epsilon = 0.100, 目标攻击成功率：0.11% epsilon = 0.500, 目标攻击成功率：45.56% epsilon = 1.000, 目标攻击成功率：65.64%

类别: 船，类别编号: 8 epsilon = 0.001, 目标攻击成功率：1.36% epsilon = 0.005, 目标攻击成功率：11.30% epsilon = 0.010, 目标攻击成功率：12.97% epsilon = 0.050, 目标攻击成功率：3.14% epsilon = 0.100, 目标攻击成功率：2.09% epsilon = 0.500, 目标攻击成功率：43.93% epsilon = 1.000, 目标攻击成功率：51.46%

类别: 卡车，类别编号: 9 epsilon = 0.001, 目标攻击成功率：4.25% epsilon = 0.005, 目标攻击成功率：28.19% epsilon = 0.010, 目标攻击成功率：44.25% epsilon = 0.050, 目标攻击成功率：17.51% epsilon = 0.100, 目标攻击成功率：4.97% epsilon = 0.500, 目标攻击成功率：36.99% epsilon = 1.000, 目标攻击成功率：52.12%

目标类别自身攻击特殊性：对目标类别（汽车，编号 1）的原始样本，低扰动（epsilon=0.001-0.01）时攻击成功率达 100%，因样本本身已被正确分类为目标类别。
扰动强度影响呈非单调趋势：低扰动（0.001-0.01）时成功率有类别差异（如卡车达 44.25%）；中等扰动（0.05-0.1）时普遍下降；高扰动（0.5-1）时显著回升，马在 epsilon=1.0 时达 65.64%。
类别相似性影响攻击敏感性：与目标类别（汽车）特征相似的类别（如卡车、船）更易被攻击，低扰动下成功率显著高于其他类别。
模型鲁棒性存在类别依赖：不同类别抗扰能力差异明显，如马在高扰动下最脆弱，船相对更稳定。

攻击示例如下，深蓝色代表攻击成功

FGSM无目标攻击

epsilon_list = [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1]  # 可根据需要调整

results = {class_name: [] for class_name in class_names}

# 遍历每个类别进行攻击
for i in range(10):  # CIFAR-10 共有10个类别
    print(f"类别: {class_names[i]}，类别编号: {i}")

    for epsilon in epsilon_list:
        # 统计攻击成功率
        success = 0
        total = 0

        for data, label in test_loader:
            data, label = data.to(device), label.to(device)

            # 初始预测
            output = model(data)
            init_pred = output.max(1, keepdim=True)[1]

            # 初始预测
            output = model(data)
            init_pred = output.max(1, keepdim=True)[1]

            # 仅对属于当前测试类别且初始预测正确的样本进行攻击
            correct_indices = (init_pred.squeeze() == label) & (label == i)
            if correct_indices.sum().item() == 0:
                continue

            data = data[correct_indices]
            label = label[correct_indices]


            # 对每个样本进行FGSM无目标攻击
            perturbed_data = fgsm_untargeted_attack(model, device, data, label, epsilon)

            # 测试对抗样本
            output = model(perturbed_data)
            final_pred = output.max(1, keepdim=True)[1]

            # 统计成功将模型误导到其他类别的样本数量
            success += (final_pred.squeeze() != label).sum().item()
            total += data.size(0)

            # 控制测试样本数量（1000张图片）
            if total >= 1000:
                break
        success_rate = 100 * success / total if total > 0 else 0
        print(f"epsilon = {epsilon:.3f}, 无目标攻击成功率：{success_rate:.2f}%")
        results[class_names[i]].append(success_rate)
    print("\n")

类别: 飞机，类别编号: 0 epsilon = 0.001, 无目标攻击成功率：15.82% epsilon = 0.005, 无目标攻击成功率：65.07% epsilon = 0.010, 无目标攻击成功率：84.50% epsilon = 0.050, 无目标攻击成功率：99.26% epsilon = 0.100, 无目标攻击成功率：100.00% epsilon = 0.500, 无目标攻击成功率：100.00% epsilon = 1.000, 无目标攻击成功率：100.00%

类别: 汽车，类别编号: 1 epsilon = 0.001, 无目标攻击成功率：7.22% epsilon = 0.005, 无目标攻击成功率：38.18% epsilon = 0.010, 无目标攻击成功率：59.00% epsilon = 0.050, 无目标攻击成功率：89.02% epsilon = 0.100, 无目标攻击成功率：96.23% epsilon = 0.500, 无目标攻击成功率：65.48% epsilon = 1.000, 无目标攻击成功率：48.22%

类别: 鸟，类别编号: 2 epsilon = 0.001, 无目标攻击成功率：21.75% epsilon = 0.005, 无目标攻击成功率：64.82% epsilon = 0.010, 无目标攻击成功率：74.03% epsilon = 0.050, 无目标攻击成功率：70.70% epsilon = 0.100, 无目标攻击成功率：48.39% epsilon = 0.500, 无目标攻击成功率：36.96% epsilon = 1.000, 无目标攻击成功率：56.49%

类别: 猫，类别编号: 3 epsilon = 0.001, 无目标攻击成功率：31.24% epsilon = 0.005, 无目标攻击成功率：81.78% epsilon = 0.010, 无目标攻击成功率：87.93% epsilon = 0.050, 无目标攻击成功率：77.40% epsilon = 0.100, 无目标攻击成功率：80.59% epsilon = 0.500, 无目标攻击成功率：100.00% epsilon = 1.000, 无目标攻击成功率：100.00%

类别: 鹿，类别编号: 4 epsilon = 0.001, 无目标攻击成功率：17.44% epsilon = 0.005, 无目标攻击成功率：74.84% epsilon = 0.010, 无目标攻击成功率：86.47% epsilon = 0.050, 无目标攻击成功率：84.04% epsilon = 0.100, 无目标攻击成功率：95.24% epsilon = 0.500, 无目标攻击成功率：100.00% epsilon = 1.000, 无目标攻击成功率：100.00%

类别: 狗，类别编号: 5 epsilon = 0.001, 无目标攻击成功率：18.40% epsilon = 0.005, 无目标攻击成功率：69.26% epsilon = 0.010, 无目标攻击成功率：81.26% epsilon = 0.050, 无目标攻击成功率：98.51% epsilon = 0.100, 无目标攻击成功率：100.00% epsilon = 0.500, 无目标攻击成功率：100.00% epsilon = 1.000, 无目标攻击成功率：100.00%

类别: 青蛙，类别编号: 6 epsilon = 0.001, 无目标攻击成功率：15.52% epsilon = 0.005, 无目标攻击成功率：72.54% epsilon = 0.010, 无目标攻击成功率：89.97% epsilon = 0.050, 无目标攻击成功率：76.45% epsilon = 0.100, 无目标攻击成功率：81.52% epsilon = 0.500, 无目标攻击成功率：100.00% epsilon = 1.000, 无目标攻击成功率：100.00%

类别: 马，类别编号: 7 epsilon = 0.001, 无目标攻击成功率：14.48% epsilon = 0.005, 无目标攻击成功率：64.59% epsilon = 0.010, 无目标攻击成功率：84.14% epsilon = 0.050, 无目标攻击成功率：98.94% epsilon = 0.100, 无目标攻击成功率：100.00% epsilon = 0.500, 无目标攻击成功率：100.00% epsilon = 1.000, 无目标攻击成功率：100.00%

类别: 船，类别编号: 8 epsilon = 0.001, 无目标攻击成功率：8.79% epsilon = 0.005, 无目标攻击成功率：43.51% epsilon = 0.010, 无目标攻击成功率：52.20% epsilon = 0.050, 无目标攻击成功率：85.15% epsilon = 0.100, 无目标攻击成功率：99.90% epsilon = 0.500, 无目标攻击成功率：100.00% epsilon = 1.000, 无目标攻击成功率：100.00%

类别: 卡车，类别编号: 9 epsilon = 0.001, 无目标攻击成功率：8.70% epsilon = 0.005, 无目标攻击成功率：47.46% epsilon = 0.010, 无目标攻击成功率：67.25% epsilon = 0.050, 无目标攻击成功率：90.26% epsilon = 0.100, 无目标攻击成功率：98.96% epsilon = 0.500, 无目标攻击成功率：100.00% epsilon = 1.000, 无目标攻击成功率：100.00%

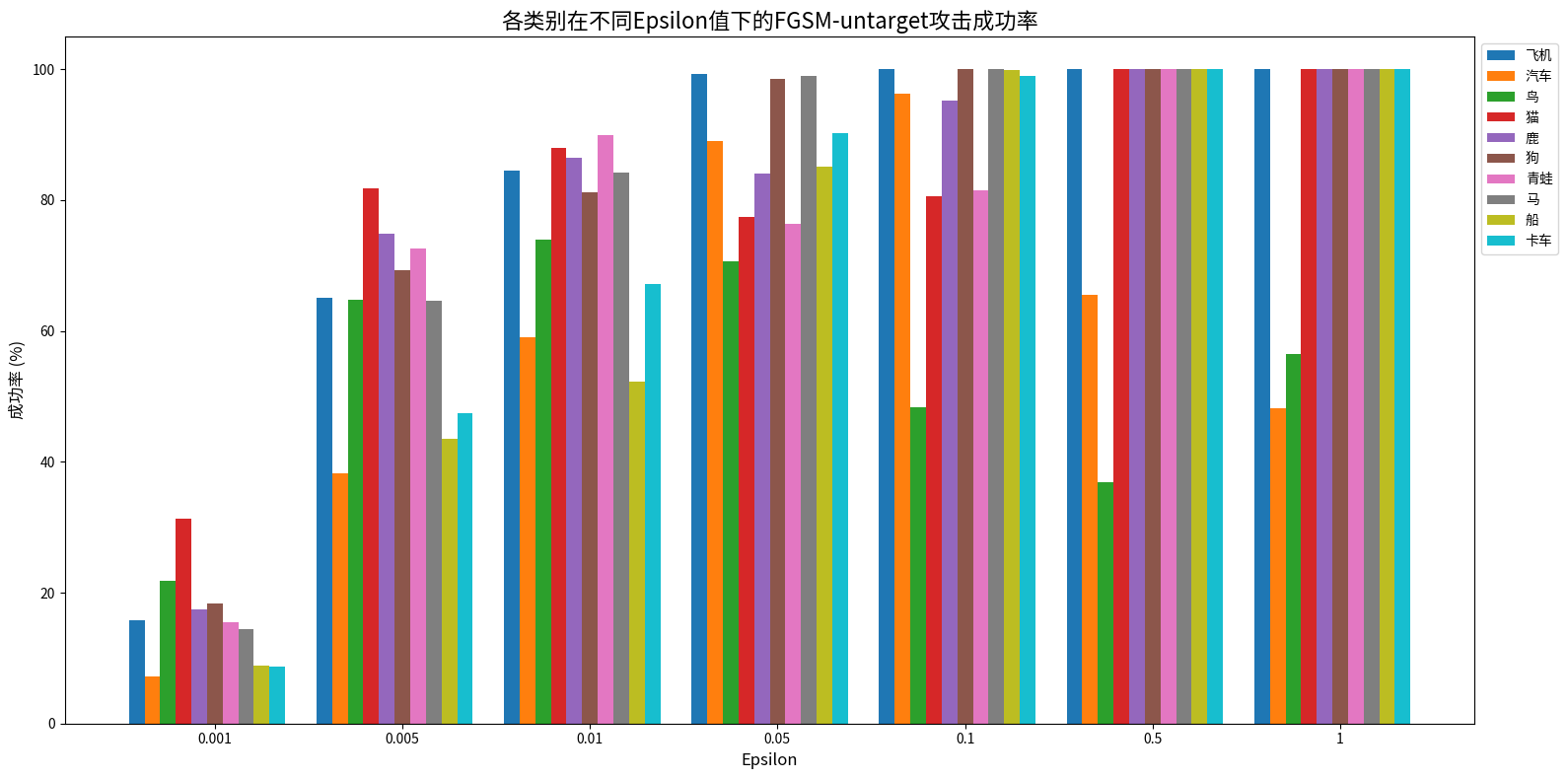
多数类别成功率随 epsilon 增大呈 “上升 - 稳定”，中等及以上扰动基本达 100%。
低扰动（0.001）时，猫最易攻击（31.24%），汽车 / 船 / 卡车最抗扰（7%-9%）。
汽车、鸟特殊：高扰动下成功率下降（如汽车从 96.23% 降至 48.22%）。
除汽车、鸟外，8 类在 epsilon≥0.5 时成功率均为 100%。

攻击示例如下，红色字体代表攻击成功

可视化对比

# 绘制条形图
def plot_results(results, epsilon_list,target=True):
    num_classes = len(results)
    bar_width = 0.1  # 柱宽
    spacing = 0.2  # 每个 epsilon 之间的间隔
    index = [x * (1 + spacing) for x in range(len(epsilon_list))]  # 在X轴上为每个epsilon留出间隔

    plt.figure(figsize=(16, 8))
    
    # 对每个类别绘制柱状图
    for i, (class_name, success_rates) in enumerate(results.items()):
        plt.bar([x + i * bar_width for x in index], success_rates, bar_width, label=class_name)

    # 设置X轴标签为epsilon值
    plt.xlabel('Epsilon', fontsize=12)
    plt.ylabel('成功率 (%)', fontsize=12)
    plt.xticks([r + (num_classes / 2) * bar_width for r in index], epsilon_list)
    if target==True:
        plt.title('各类别在不同Epsilon值下的FGSM-target攻击成功率,1为target', fontsize=16)
    else:
        plt.title('各类别在不同Epsilon值下的FGSM-untarget攻击成功率', fontsize=16)
    plt.legend(loc='upper left', bbox_to_anchor=(1, 1))
    plt.tight_layout()
    plt.show()

有目标攻击

1	`plot_results(results_target, epsilon_list)`

无目标攻击

1 2	`# 调用绘图函数 plot_results(results, epsilon_list,target=False)`

攻击难度：有目标攻击更难实现有目标攻击（需定向误导至特定类别）整体成功率显著低于无目标攻击（仅需误分类）。例如：
- 低扰动（epsilon=0.01）时，卡车（类别 9）的有目标成功率为 44.25%，无目标则达 67.25%；
- 中等扰动（epsilon=0.1）时，飞机（类别 0）有目标成功率 1.38%，无目标达 100%。
  
  核心原因：有目标攻击受限于特定目标类别，而无目标攻击可 “任意误分类”，容错空间更大。
扰动强度影响趋势不同
- 有目标攻击：成功率随 epsilon 呈 “低 - 中降 - 高升” 的非单调趋势（中等扰动时普遍下降）；
- 无目标攻击：多数类别呈 “稳步上升 - 高扰动稳定” 趋势（中等扰动后快速达 100%）。
类别特殊性表现差异
- 有目标攻击中，目标类别自身（汽车）在低扰动时成功率 100%（无需扰动），是唯一特例；
- 无目标攻击中，汽车、鸟表现异常：高扰动下成功率下降（如汽车从 96.23% 降至 48.22%），与其他类别 “高扰动稳定 100%” 不同。
高扰动下的共性与差异
- 共性：高扰动（epsilon≥0.5）时，两类攻击对多数类别的成功率均显著提升；
- 差异：无目标攻击中 8 类达 100%，而有目标攻击最高为 65.64%（马），仍受限于目标类别约束。

总结与心得

通过本次对抗攻击实验，我认识到神经网络模型在面对精心设计的微小扰动时表现出的脆弱性。实验表明，即使训练准确率超过92%的ResNet-20模型，在ε=0.01的微小扰动下，多数类别的无目标攻击成功率已超过80%。有目标攻击虽然更难实现，但在高扰动下仍能达成定向误导。

AI攻防

#FGSM #CIFAR-10 #ResNet-20

神经网络模型FGSM攻击实践

http://horizongazer.github.io/2025/10/18/神经网络模型FGSM攻击实践/

作者

HorizonGazer

发布于

2025年10月18日

许可协议

神经网络模型对抗防御实践上一篇

完全信息动态博弈之Stackelberg Game 下一篇